
TAM GIÁC 227
(tamgiac227.*)
Cho tam giác ABC có tọa độ 3 đỉnh là \(A(x_{a},\ y_{a}),\ B(x_{b},\ y_{b}),C(x_{c},\ y_{c})\) như hình.
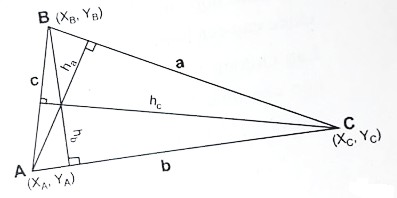
Hãy tính:
+ Diện tích tam giác ABC.
+ Độ dài các đường cao \(h_{a},\ h_{b},\ h_{c}\)
Dữ liệu vào: 6 số nguyên \(x_{a},\ y_{a},\ x_{b},\ y_{b},\ x_{c},\ y_{c}\)
Giới hạn: các số nhập vào có giá trị tuyệt đối không quá 1000
Kết quả:
+ Dòng đầu ghi diện tích tam giác ABC
+ Dòng thứ 2 lần lượt ghi độ dài các đường cao \(h_{a},\ h_{b},\ h_{c}\)
Các số được ghi với độ chính xác 3 chữ số thập phân
Biết rằng:
+ Công thức Hê-rông tính diện tích tam giác: \(S = \sqrt{p(p - a)(p - b)(p - c)}\) trong đó \(a,\ b,\ c\) là độ dài 3 cạnh tam giác, \(p = (a + b + c)/2\)
+ Độ dài \(d\) của đoạn thẳng nối 2 điểm có tọa độ \((x,y)\) và \((u,v)\) trong mặt phẳng được tính theo công thức \(d = \sqrt{(x - u)^{2} + (y - v)^{2}}\)
Ví dụ:
| Input | Output |
|---|---|
| -9 11 -3 5 -3 -4 | 27.000 6.000 3.343 6.364 |
Bạn cần đăng nhập để nộp bài
| Code tích cực |
|---|
| Trong 24h |
| Trong 7 ngày |
|
| Trong 30 ngày |
|
| Thống kê |
|---|
|
AC/Sub: 97887/180710 Pascal: 17121 C++: 130348 Python: 33199 Lượt xem/tải tests: 38905 |
