
DIỆN TÍCH PHỦ
Diện tích phủ (covering.*)
 Mệt
mỏi vì có quá nhiều bài tập về nhà, Bắc tiện tay lấy tập giấy màu thủ
công của em Ninh và cắt thành \(n\)
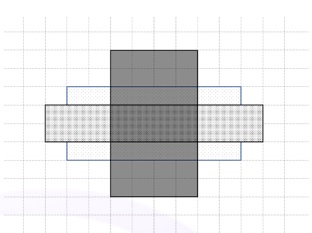
hình chữ nhật có cạnh là các số chẵn. Các hình chữ nhật sau đó được dán
chồng lên nhau sao cho các cạnh của chúng song song với các trục tọa độ
và tâm của tất cả \(\mathbf{n}\) hình
chữ nhật trùng nhau.
Mệt
mỏi vì có quá nhiều bài tập về nhà, Bắc tiện tay lấy tập giấy màu thủ
công của em Ninh và cắt thành \(n\)
hình chữ nhật có cạnh là các số chẵn. Các hình chữ nhật sau đó được dán
chồng lên nhau sao cho các cạnh của chúng song song với các trục tọa độ
và tâm của tất cả \(\mathbf{n}\) hình
chữ nhật trùng nhau.
Kết quả là Bắc có một hình đa giác đầy màu sắc. Vốn là một học sinh chuyên Toán, Bắc muốn thư giãn bằng cách tìm diện tích hình đa giác kì lạ của mình.
Yêu cầu: Cho \(n\) hình chữ nhật có độ lớn các cạnh tương ứng là \(w\) và \(h\) (\(w\) và \(h\) chẵn). Tìm diện tích phủ bởi \(n\) hình chữ nhật khi xếp chúng như mô tả.
Dữ liệu vào:
Dòng đầu tiên chứa số nguyên \(n\left( 1 \leq n \leq 10^{5} \right)\).
Dòng thứ \(i\) trong \(n\) dòng tiếp theo chứa 2 số nguyên chẵn \(w_{i},h_{i}\left( 2 \leq w_{i},h_{i} \leq 10^{9} \right)\) – tương ứng chiều rộng và chiều cao của hình chữ nhật thứ \(i\).
Kết quả: Một số nguyên là kết quả bài toán.
Ví dụ:
| Input | Output | |
|---|---|---|
| 3 4 8 8 4 10 2 | 52 |
Ràng buộc: 50% số test có \(\mathbf{n},\ \mathbf{w}_{\mathbf{i}},\ \mathbf{c}_{\mathbf{i}} \leq \mathbf{100}\)
Bạn cần đăng nhập để nộp bài
| Code tích cực |
|---|
| Trong 24h |
|
| Trong 7 ngày |
|
| Trong 30 ngày |
|
| Kỳ thi |
|---|
| Lập trình cơ bản |
| Luyện thi Chuyên Tin - CB |
| Luyện thi Chuyên Tin - NC |
| Tuyển tập Đề thi Tuyển sinh 10 |
| Tuyển tập Đề thi HSG THCS |
| Tuyển tập Đề thi HSG THPT |
| Tuyển tập Đề thi HSG Chọn đội tuyển |
| Thống kê |
|---|
|
AC/Sub: 120817/226949 Pascal: 18142 C++: 157988 Python: 50747 Lượt xem/tải tests: 41122 |
