
CHI PHÍ NHỎ NHẤT
(mcwv.*)
Cho đồ thị vô hướng liên thông có \(n\) đỉnh và \(m\) cạnh.
Yêu cầu: Hãy cho biết độ dài đường đi ngắn nhất từ đỉnh \(s\) bắt buộc đi qua đỉnh \(v\) rồi đến đỉnh \(t\). Biết rằng độ dài của một đường đi là tổng trọng số của các cạnh trên đường đi đó sao cho trọng số của một cạnh được cộng vào đúng một lần.
Dữ liệu vào:
+ Dòng đầu tiên ghi 2 số nguyên dương \(n,m\ (1 \leq n \leq 10^{5};n \leq m \leq min(10^{5},\frac{n(n - 1)}{2})\).
+ Dòng thứ hai ghi lần lượt 3 số \(s,\ t,\ v\ (1 \leq s,t,v \leq n)\)
+ \(m\) dòng tiếp theo, mỗi dòng ghi 3 số nguyên lần lượt là \(x,\ y,c\ (1 \leq x,y < n;1 \leq c \leq 10^{9})\) cho biết cạnh \(x,\ y\) có trọng số \(c\).
Dữ liệu ra:
+ Một số nguyên duy nhất cho biết kết quả của bài toán.
| Input | Output | |
|---|---|---|
| 4 3 1 3 4 1 2 1 2 3 2 2 4 3 | 6 | 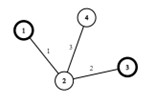 |
Ràng buộc:
+ Có 20% số test có \(s = t\)
+ Có \(60\%\) số test khác có kết quả là độ dài của đường đi đơn.
+ Có 20% số test còn lại không ràng buộc gì thêm.
Bạn cần đăng nhập để nộp bài
| Code tích cực |
|---|
| Trong 24h |
| Trong 7 ngày |
|
| Trong 30 ngày |
|
| Kỳ thi |
|---|
| Lập trình cơ bản |
| Luyện thi Chuyên Tin - CB |
| Luyện thi Chuyên Tin - NC |
| Tuyển tập Đề thi Tuyển sinh 10 |
| Tuyển tập Đề thi HSG THCS |
| Tuyển tập Đề thi HSG THPT |
| Tuyển tập Đề thi HSG Chọn đội tuyển |
| Thống kê |
|---|
|
AC/Sub: 120817/226949 Pascal: 18142 C++: 157988 Python: 50747 Lượt xem/tải tests: 42082 |
