
QUÂN MÃ
Xét lưới ô vuông vô hạn trong đó có một số ô cấm, các ô còn lại là tự do. Các dòng và cột của lưới được đánh số theo thứ tự bởi các số nguyên …-3 -2 -1 0 1 2 3 … Các cột được đánh số từ trái sang phải, còn các dòng theo thứ tự từ dưới lên trên. Ô nằm trên giao của dòng \(x\) và cột \(y\) được gọi là ô \((x,y)\). Một quân mã đặt ở ô xuất phát là ô \((0,0)\). Sau một bước đi, ta có thể di chuyển quan mã đến một trong các ô ở đỉnh đối diện trên đường chéo của hình chữ nhật kích thước \(2 \times 3\).
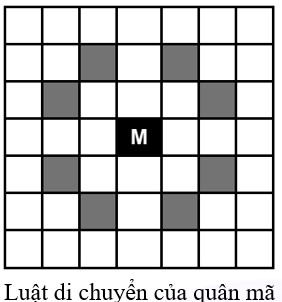
Luật di chuyển của quân mã
Yêu cầu: Cho biết tọa độ của các ô cấm, vị trí ô đích nơi quan mã cần đến, hãy tìm cách di chuyển quân mã từ ô \((0,0)\) đến ô đích sao cho số lượng bước đi cần thực hiện là ít nhất.
Dữ liệu vào:
+ Dòng đầu chứa \(t\ (t \leq 3)\) là số lượng test, tiếp theo là \(t\) nhóm dòng, mỗi nhóm chứa dữ liệu về một test theo khuôn dạng sau:
Dòng đầu tiên chứa 2 số nguyên \(x_{t},\ y_{t}\) được ghi cách nhau bởi dấu cách cho biết tọa độ của ô đích là \((x_{t},\ y_{t})\);
Dòng thứ hai chứa số nguyên dương \(n\) \((n \leq 1000)\) là số lượng ô cấm;
Dòng thứ \(i\) trong số \(n\) dòng tiếp theo chứa hai số ngueyen được ghi cách nhau một dấu cách \(x_{i},\ y_{i}\) cho biết \((x_{i},y_{i})\) là tọa độ của ô cấm thứ \(i\) \((i = 1,2,\ldots,n)\).
Kết quả: Gồm \(t\) dòng, mỗi dòng chứa kết quả của một test tương ứng trong dữ liệu vào là số lượng bước đi ít nhất cần thực hiện để di chuyển quân mã từ ô xuất phát \((0,0)\) đến ô đích. Ghi số \(- 1\) nếu như không thể di chuyển quân mã đến ô đích.
Ví dụ:
| Input | Output |
|---|---|
| 1 2 4 0 | 2 |
Ràng buộc:
+ có 50% số test có \(- 10^{3} \leq x_{t},\ y_{t} \leq 10^{3};\ - 10^{3} \leq x_{i},\ y_{i} \leq 10^{3};\)
+ có 50% số test khác có \(n = 0\) và \(- 10^{9} \leq x_{t},\ y_{t} \leq 10^{9}.\)
Bạn cần đăng nhập để nộp bài
| Code tích cực |
|---|
| Trong 24h |
|
| Trong 7 ngày |
|
| Trong 30 ngày |
|
| Kỳ thi |
|---|
| Lập trình cơ bản |
| Luyện thi Chuyên Tin - CB |
| Luyện thi Chuyên Tin - NC |
| Tuyển tập Đề thi Tuyển sinh 10 |
| Tuyển tập Đề thi HSG THCS |
| Tuyển tập Đề thi HSG THPT |
| Tuyển tập Đề thi HSG Chọn đội tuyển |
| Thống kê |
|---|
|
AC/Sub: 120817/226949 Pascal: 18142 C++: 157988 Python: 50747 Lượt xem/tải tests: 41115 |
