
CÂY CON CHUNG LỚN NHẤT
1. Đề bài
Cho 2 cây \(T_{1}\) và \(T_{2}\) mỗi cây có \(n\) nút. Cây \(T_{1}\) có nút gốc là \(r_{1}\), cây \(T_{2}\) có nút gốc là \(r_{2}\), Các nút trên cây được đánh số thứ tự từ 1 đến \(n\). Hãy tìm cây con chung của \(T_{1}\) và \(T_{2}\) sao cho số nút của cây con chung là lớn nhất.
Biết rằng cây \(St\) (có nút gốc \(r_{st}\)) được gọi là cây con của cây \(T\) (có nút gốc \(r_{t}\)) khi thỏa một trong hai điều kiện:
1. \(St\ \)giống \(T\) hoàn toàn.
2. Từ \(T\) có thể loại bỏ 1 cung \((u,v)\) sao cho \(T\) trở thành 2 cây: cây thứ nhất có nút gốc \(r_{t}\), cây thứ 2 có nút gốc \(v\). Trong đó cây thứ 2 giống hoàn toàn cây \(St\).
Ví dụ:
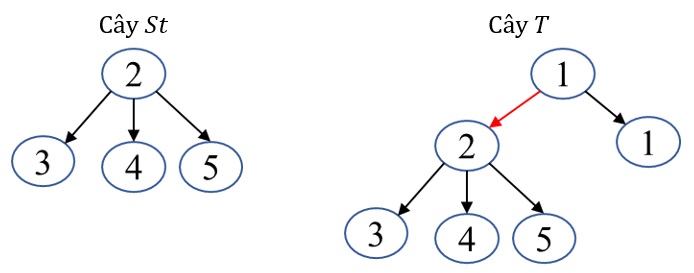
| Cây \(St\) | Cây \(T\) | |
|---|---|---|
 |
 |
Ở hình trên cây \(St\) là cây con của cây \(T\) vì khi xóa cung \((1,2)\) thu được cây có gốc \(v = 2\) giống cây \(St\).
Dữ liệu vào:
+ Dòng đầu ghi số nguyên dương \(n\ (1 \leq n \leq 10^{5})\) là số nút của mỗi cây.
+ Dòng thứ hai ghi số nguyên \(r_{1}\ (1 \leq r_{1} \leq n)\) là nút gốc của cây thứ nhất.
+ \(n - 1\) dòng tiếp theo, mỗi dòng ghi 2 số nguyên \(u,\ v\) cho biết 1 cung trên cây \(T_{1}\), trong đó \(u\) là “cha” của \(v\).
+ Dòng tiếp theo ghi số nguyên \(r_{2}\ (1 \leq r_{2} \leq n)\) là nút gốc của cây thứ hai.
+ \(n - 1\) dòng tiếp theo, mỗi dòng ghi 2 số nguyên \(u,\ v\) cho biết 1 cung trên cây \(T_{2}\), trong đó \(u\) là “cha” của \(v\).
Kết quả: Một số nguyên duy nhất cho biết số nút của cây con chung lớn nhất của hai cây \(T_{1}\) và \(T_{2}\).
Ví dụ:
| Input | Output | Giải thích |
|---|---|---|
| 6 6 2 5 3 2 5 1 5 4 6 3 6 2 5 5 1 5 4 6 3 6 2 | 4 | Cây con chung là 2 5 5 1 5 4 Gồm 4 nút {2, 5, 1, 4} |
Bạn cần đăng nhập để nộp bài
| Code tích cực |
|---|
| Trong 24h |
| Trong 7 ngày |
|
| Trong 30 ngày |
|
| Kỳ thi |
|---|
| Lập trình cơ bản |
| Luyện thi Chuyên Tin - CB |
| Luyện thi Chuyên Tin - NC |
| Tuyển tập Đề thi Tuyển sinh 10 |
| Tuyển tập Đề thi HSG THCS |
| Tuyển tập Đề thi HSG THPT |
| Tuyển tập Đề thi HSG Chọn đội tuyển |
| Thống kê |
|---|
|
AC/Sub: 120817/226949 Pascal: 18142 C++: 157988 Python: 50747 Lượt xem/tải tests: 42082 |
